참고자료 : MultimediaSystemBook_20230424, 박규식교수님 수업자료
Image compression
- 이미지 압축의 목적 : 저장비용(cost for storage)과 전송비용(cost for transmission) 줄임
- 이미지 압축의 종류 :
- 비손실 압축(Lossless) : 손실은 없음, 압축률(compression ratio)가 낮다 / PNG, PCX
- 손실압축(Lossy) : 허용가능한 손실, 압축률이 높다 / DCT, JPEG, JPEG2000
- 주파수 영역에서의 분석( 이미지압축 프로세스의 필수과정 )기본적으로 일반 데이터에 대해서 Time-domain waveform( time-amplitude )을 저장 → FFT알고리즘을 적용하여 Frequency-domain spectrum( frequency(Hz)-magnitude )을 도출

- 이미지 인식 = 공간주파수 분석( spatial frequency )
: 픽셀단위의 2D상 이미지에서 배경은 낮은 주파수요소로, 경계선은 높은 주파수 요소로 인식
DCT( discrete cosine transform )
: 이미지의 픽셀 데이터를 주파수 데이터로 변경 ( Time-frequency transform = Spatial-frequency transfrom ) ⇒ DCT spectral coefficients( 주파수 성분들 ) 도출하는 일종의 압축 알고리즘, JPEG 압축과정의 핵심 알고리즘
- Energy compation: 대부분의 에너지(90%)는 저주파영역(low freq.area)에 집중되더있음 & 고주파 영역(high freq.area)에는 적게 집중
- Bit allocation : 이러한 에너지분포에 따라 비트를 할당높은 주파수, 작은 에너지에 더 적은 비트 할당 ⇒ 최종적으로 비트수를 아낌 = 즉 낮은 주파수, 큰 에너지에 더 많은 비트 할당( 모두 동일한 24bit할당X )
- zigzag pattern read로 나열 = 저주파에서 고주파 성분값을 나열

DCT를 취하였을때,
DC성분 : 주파수가 0일때, 맨왼쪽 성분 ↔ AC성분 : 주파수가 0이상, 이외성분
DC에서 AC오른쪽 하단으로 내려갈수록(주파수가 높아질수록) 픽셀값(부호무시한 크기값=절대값)이 점점 낮아짐

JPEG
1992년 표준화된 압축알고리즘( ISO/IEC JTC1 SC29 WG1 )으로 이미지 데이터를 약 10:1 정도로 압축이 가능하다.
[ JPEG Encoder ]
:: hybrid coding(혼합코딩) = DCT coding + DPCM, RLC, Entropy coding

(1) Image preparation
- RGB color model → YCbCr color model 변환
- 각 채널을 MB(Macro block)단위로 표현 (8X8)
(2) DCT : 8X8 MB단위 spatial-domain pixels(f) ⇒ 8X8 frequency-domain pixels(F)
(ex) DC값인 F(0,0) => 235.6

(3) Quantization
Round ( DCT coefficients/quantization table ) ⇒ Quantized DCT coefficients도출
: 저주파값들은 큰 값으로 & 고주파값들은 작아지거나 0으로 수렴
- Quantization table( 나누는 값 ) : 압축비율을 조정하는 핵심역할!
Q.table의 값이 커짐 = 높은 압축률 & Q.table의 값이 작아짐 = 낮은 압축률( 이미지 quality는 좋음 ) - DC영역의 값이 상대적으로 작음 → 고주파영역의 값으로 갈수록 값이 커짐
- Quantized DCT coefficients : DC요소에 가장 큰 값, AC요소는 고주파로 갈수록 값이 점점 작아짐(0에 수렴)
(ex) round(-415.38/16)=-26 & round(-30.19/11)=-3


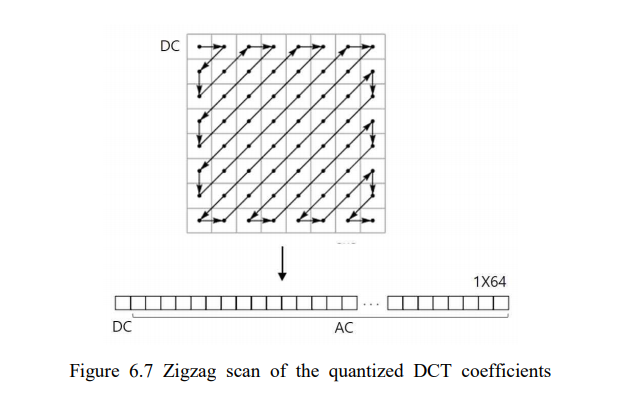
(4) ZigZag scan
: Quantized DCT coefficients의 일차원화 / 2D Quantized DCT(8X8) ⇒ 1D vectors(1X64)
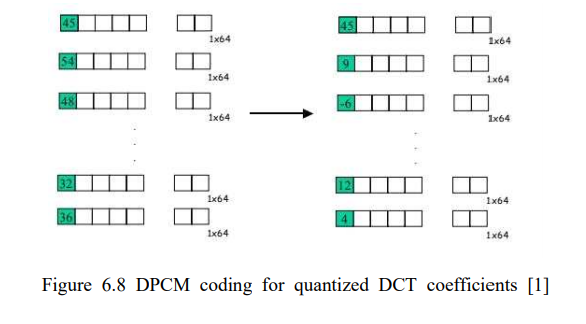
(5) DPCM coding for DC & RLE(RLC) coding for AC
- Quantized DCT coefficients = 1 DC + 63 AC
- DC는 DPCM( different PCM ) coding : 각 MB단위의 DC값이 유사하다면 이웃한 MB들의 차이만 코딩( 기준 DC는 원본값 그대로 코딩 )
- AC는 RLE( Run length encoding )
AC값들은 반복되는 숫자가 많음 → 반복숫자를 counting하여 코딩, bit saving!
(6) Entropy coding : Huffman coding을 수행
(7) 최종결과물 : Data(압축 데이터, binary bit) + header( n번째 MB ) + tables( Q테이블, Entropy tables )
[ JPEG Decoder ]
: JPEG Encoder와 반대로 동작
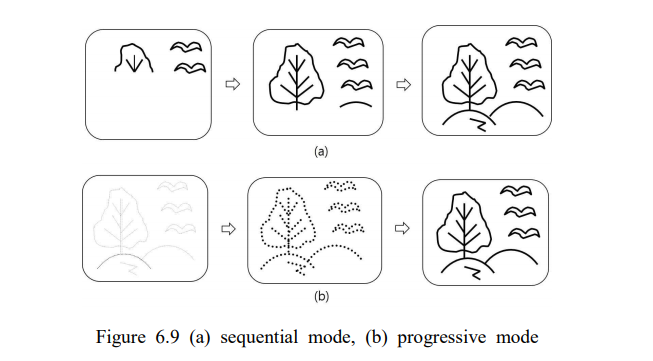
- Sequential mode : 순차적으로 압축된 이미지를 디스플레이
- Progressive mode : 전체적으로 압축된 이미지 디스플레이, 해상도가 낮은 것부터 시작해서 높은 것으로 디스플레이
JPEG 2000
- JPEG보다 높은 압축률, 높은 품질 ⇒ 그럼에도 JPEG이 주류로 이용
- JPEG은 DCT기반 ↔ JPEG2000은 wave-let기반( 더 나은 사양의 하드웨어(프로세서)가 요구됨, 벤더사들의 플랫폼 변경이 요구됨 )

Image Processing
Post correction( 후보정 ) : 경계선강화, 잡음제거, 밝기/색상 변경의 작업 → 다양한 기술과 알고리즘이 사용됨
- MATLAB의 IPT( image processing toolbox : 이미지 분야에서 사용되는 빌트인 라이브러리들 )을 적절하게 활용

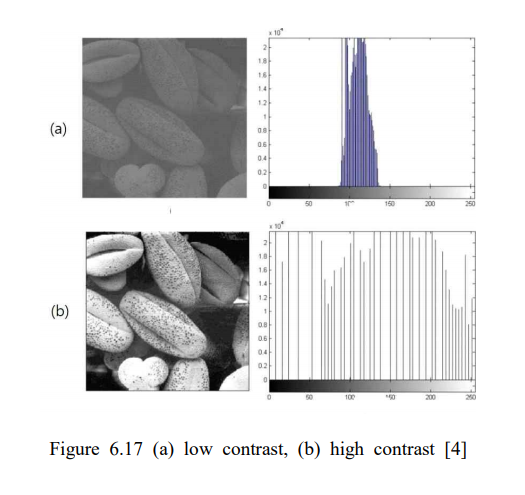
(1) Histogram equalization = 대비개선
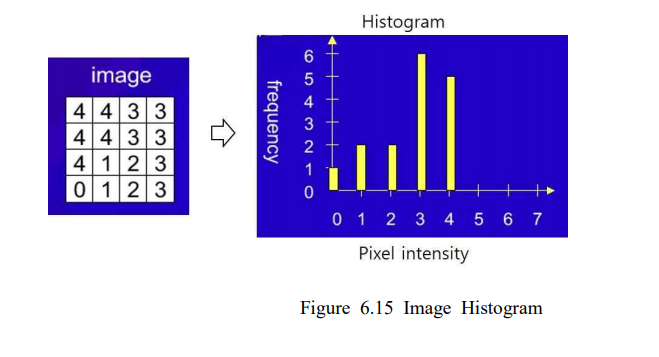
- Histogram : 각 픽셀값(밝기)의 빈도수를 표현( imhist ), grayscale = 0~255
- 어두운 이미지( low key ) : 왼쪽 부분에 분포 ↔ 밝은 이미지( high key ) : 오른쪽 부분에 분포
⇒ 적절한 대조(contrast)가 필요 ( 사물식별을 수월하기위한 밝기, 색상의 차이 )

- Histogram equalization : 히스토그램의 분포를 균일하게 함 ⇒ 이미지의 대조높임( histeq )
- True color img(RGB)의 대비개선
- 1) 채널별로(R, G, B) 분리하여 equalization을 실행하고 통합 → 균형이 망가짐
-

- 2) RGB → HSV or YCbCr로 transform( rgb2hsv(w) ) → luminance채널(V, Y)에 equalization을 실행하고 통합( histeq(w(:,:,3)) )
명도채널만 균등화 → 원본이미지의 색상균형을 유지하면서 대비를 향상


(2) Spatial filtering ( convolution ) : 특정 필터의 적용 -> 이웃한 픽셀들의 가중합( weighted sum )
- element & element multiplication → sum :: 맨왼쪽부터 시작하여 오른쪽으로 shift하며 가중합 연산
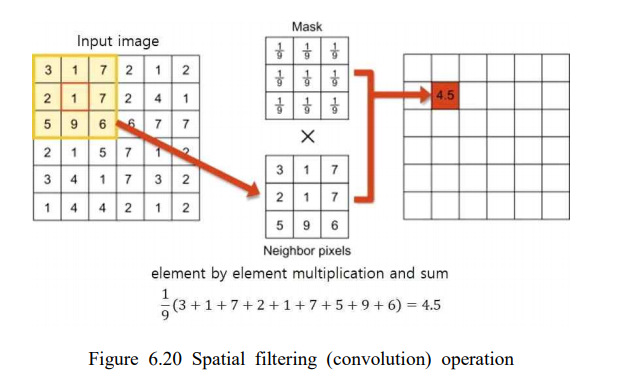
weight = mask = filter = kernel = template 의 종류
- LPF( low pass filter ) : 이미지의 저주파 성분(배경)만 통과, 고주파 성분(경계, 거친 잡음)은 제거
⇒ blurring( 경계선이 제거 ), 부드럽고 따뜻한 느낌고주파 성분을 평균값으로 바꾸는 효과 = 픽셀간 차이를 완화(평균화)
이때 필터의 계수값의 총합은 1을 유지한다( 픽셀크기에 따라 정해짐 : nxn은 모두 1/nxn )

- HPF( hig pass filter ) : 이미지의 고주파 성분(경계, 잡음)만 통과, 저주파 성분(배경)은 통과
⇒ sharpening( 경계선 강조 ), 선명해짐
이때도 계수값의 총합이 1을 유지한다 : -1을 채우고 +양수

- imfilter( 이미지, 정의한 필터 ) : 해당 이미지에 필터를 씌우는 MATLAB 함수
- 필터값은 계수의 합이 1이 된다 = 필터링된 값이 범위초과하는 것을 막음 = energy preservation
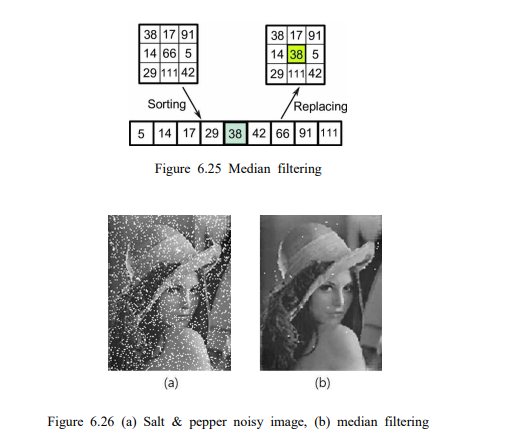
(3) Noise filtering
- Noise : salt&pepper( 흩어진 노이즈 ), Gaussian noise( 문드러진 효과 )
=> imnoise함수로 인위적으로 생성가능

- median filter : 각 픽셀값을 읽어 순서대로 sorting → 중간값(median)으로 대체 ⇒ salt&pepper 노이즈를 필터링
<-> mean filter : 각 픽셀값을 읽어 평균값(mean)으로 대체= LPF

(4) Edge detection : 상당한 변동값( 경계값 )을 감지 = 일종의 HPF
- 다양한 알고리즘을 이용하여 진행가능 -> edge( w, ‘Sobel’ ); edge( w, ‘Prewitt’ ); edge( w, ‘Roberts’ );

(5) interpolation : 이미지 크기의 확대 → 공백부분( unknown pixels )을 임의값으로 채움
+) imresize( 이미지, 몇배수, 알고리즘 ) : imresize( w, 2, ‘nearest’ ); imresize( w, 4, ‘bilinear’ );
- Nearest neigbor : 간단하게 가장 근접한 이웃의 픽셀값을 취함
- Bilinear : 인접한 2X2픽셀들의 거리비율(distance ratio)로 새로운 값을 추정
- Bicubic : 인접한 4X4픽셀들의 거리비율(distance ratio)로 새로운 값을 추정

(6) Image rotation & reflection
- imrotate( 이미지, 각도 );
- flipud( 이미지 ) : 위아래 뒤집기 / fliplr( 이미지 ) : 좌우뒤집기
'computer science' 카테고리의 다른 글
| [MultimediaSystem] Digital Audio Compression (0) | 2024.06.24 |
|---|---|
| [MultimediaSystem] Digital Video Compression (0) | 2024.06.24 |
| [MultimediaSystem] Color depth / Color model / Color space (0) | 2024.06.23 |
| [MultimediaSystem] Vector graphic & Bitmap image (0) | 2024.06.22 |
| [ OSTEP ] File System Advacned (0) | 2024.06.21 |