23.10.01
KNN을 이용한 간단한 분류작업( classifier )
생선 데이터셋을 직접 만들었다.
import matplotlib.pyplot as plt
#도미데이터
bream_length = [25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0, 30.0, 30.7, 31.0, 31.0, 31.5, 32.0, 32.0, 32.0, 33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0, 35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5, 39.5, 41.0, 41.0]
bream_weight = [242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0, 390.0, 450.0, 500.0, 475.0, 500.0, 500.0, 340.0, 600.0, 600.0, 700.0, 700.0, 610.0, 650.0, 575.0, 685.0, 620.0, 680.0, 700.0, 725.0, 720.0, 714.0, 850.0, 1000.0, 920.0, 955.0, 925.0, 975.0, 950.0]
#빙어데이터
smelt_length = [9.8, 10.5, 10.6, 11.0, 11.2, 11.3, 11.8, 11.8, 12.0, 12.2, 12.4, 13.0, 14.3, 15.0]
smelt_weight = [6.7, 7.5, 7.0, 9.7, 9.8, 8.7, 10.0, 9.9, 9.8, 12.2, 13.4, 12.2, 19.7, 19.9]
#도미 & 빙어 데이터 시각화
plt.scatter(bream_length, bream_weight)
plt.scatter(smelt_length, smelt_weight)
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
- 통합 데이터 생성
zip함수 : 두 개 이상의 iterable(순회 가능한 객체)을 인자로 받아, 각 iterable에서 같은 인덱스의 요소들을 묶어 새로운 iterable로 반환하는 내장 함수 (*두개의 iterable의 길이는 동일해야함)
length = bream_length + smelt_length # 두 개의 리스트를 이어붙인다!
weight = bream_weight + smelt_weight
#length, weight가 pair를 이루는 데이터
fish_data = [[l, w] for l, w in zip(length, weight)]
print(fish_data)
print(len(bream_length)) #35
print(len(smelt_length)) #14
print(len(fish_data)) #49이로써 모든 도미와 빙어의 특징정보를 담은 2차원 리스트 [l,w] 를 원소로 가지는 fish_data가 생성된다.
- 정답데이터생성 ( = target data / ground truth)
# 도미=1, 빙어=0
fish_target = [1] * len(bream_length) + [0] * len(smelt_length)
print(fish_target)- K-Nearest Neighborhood Classifier (K-최근접이웃분류 알고리즘)
: 해당 데이터와 거리(distance)가 가장 가까운 K개의 데이터를 기반으로 클래스(분류)를 예측하는 알고리즘

from sklearn.neighbors import KNeighborsClassifier
kn = KNeighborsClassifier()
kn.fit(fish_data, fish_target) #학습
kn.score(fish_data, fish_target) #성능확인
print( kn.predict([[30, 600]]) ) #예측-> 1(도미)* sklearn.neighbors = 거리기반 알고리즘을 모은 사이킷런의 하위모듈
- KNeighborsClassifier(KNN)의 메서드
fit ( 특성데이터, 해당데이터 포인트의 라벨데이터 ) : 모델을 학습시키는 메서드 (*numpy배열 혹은 리스트 형태)
predict( 특성데이터 ) : 학습된 데이터 모델로 새로운 데이터 예측 수행 -> 예측데이터 결과를 반환
score( 특성데이터, 정답데이터 ) : 특성데이터 예측결과를 정답데이터와 비교 -> 학습모델의 작동을 평가하는 점수를 반환
(* 분류문제는 0~1사이의 값 반환, 회귀문제는 -∞에서 1 사이의 값)
- 한계점 : 학습에 사용된 x데이터(kn._fit_X), y데이터(kn._fit_Y)를 기억하고 있어야한다, 거리계산에 소모가 크다.
- 하이퍼파라미터 n_neighbors : 예측을 수행할때 고려할 이웃의 수
KNN 객체 생성시 생성자에 설정
수치가 커질수록 (전체를 탐색하는 경우), 양이 많은 데이터에 의존하게 된다 => 적절한 튜닝값이 필요한 이유!
* 파라미터 : 인공지능 모델이 가진 학습가중치(weight) / 학습을 통해 개선
* 하이퍼파라미터 : 인공지능 모델을 학습하기 위해 설정하는 인위적인 값 / 관리자의 최적의 값을 찾아 튜닝작업 (Hyper-parameter Tuning)
훈련세트(trainset)와 테스트세트(testset) 분리
- 데이터셋의 구분
: 훈련세트(train set) / 검증세트(valid set) / 테스트 세트(test set)
=> Data Contamination(데이터 오염) : 테스트세트가 훈련세트에 혼합되어 성능평가를 혼동시키는 상황
- 인덱싱으로 각각 학습, 테스트 데이터 추출
train_input = fish_data[:35]
train_target = fish_target[:35]
test_input = fish_data[35:]
test_target = fish_target[35:]
kn = kn.fit(train_input, train_target) #도미데이터만 학습
print("Train 데이터셋에 대한 정확도(Train Accuracy): ", kn.score(train_input, train_target)) # 1.0
print("Test 데이터셋에 대한 정확도(Test Accuracy): ", kn.score(test_input, test_target)) # 0.0샘플링 편향(sampling bias) : 위와 같이 극단적인 데이터셋을 분리하는 경우 편향된 데이터 학습이 이루어짐( 특정 클래스의 데이터만 학습 ) -> 적절한 분배가 필요함
- scikit-learn의 train_test_split() 함수
: 특성 데이터와 대상 레이블을 주어진 비율에 따라 훈련 세트와 테스트 세트로 나누어 반환
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test =
train_test_split(fish_data, fish_target, test_size=0.28, random_state=1024, shuffle=True, stratify=fish_target)
* sklearn.model_selection: 데이터셋을 나누고 모델의 성능을 평가하기 위한 도구와 함수를 제공하는 사이킷런의 하위모듈
- 반환값
X_train(학습데이터), X_test(테스트 데이터), Y_train(학습데이터 정답), Y_test(테스트 데이터 정답) 반환
- 매개변수
1) arrays(필수 매개변수) : 데이터셋을 구성하는 특성 데이터 + 대상 레이블(또는 타겟)을 나타내는 여러 배열을 전달
2) test_size: 테스트 세트에 할당되는 크기(%) (*default = 0.25 = 25%)
3) train_size: 학습세트에 할당되는 크기(%) , test_size 지정시 자동계산 ( 1-test_size )
4) random_state: 난수 생성을 위한 시드(seed) 값
5) shuffle: 데이터를 분할하기 전에 섞을지 여부 (*default = True)
6) stratify: 클래스 사이의 비율을 유지하면서 데이터를 분할하는 옵션 , 훈련 세트와 테스트 세트 간 클래스 분포를 비슷하게 유지
데이터 전처리 (data processing)
:: 모델에 훈련 데이터를 주입하기 전에 가공하는 단계. 주로 cpu로 처리한다.
실험 ) 디폴트k=5인 모델에서 새로운데이터(25cm , 150g)의 경우 산점도가 도미에 가깝지만 빙어로 예측된다.
print(kn.predict([[25,150]])) #0(빙어)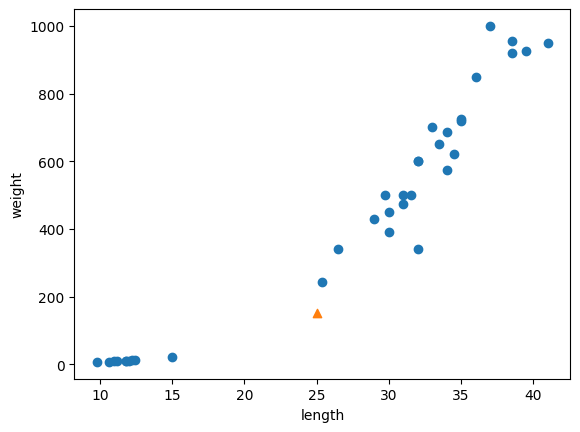
예측에 영향을 준 이웃들을 분석해보자
kn.kneighbors : 주어진 데이터 포인트와 가장 가까운 이웃 데이터 포인트들을 검색하는데 사용된다. ( 사전에 정의한 n_neighbors만큼(*default:5)의 가까운 이웃데이터들이 도출)
=> 가장가까운 데이터와의 distances, 그 데이터의 index가 순서대로 도출
= 새로운 데이터의 판별 단서가 된다.
distances, indexes = kn.kneighbors([[25, 150]])
plt.scatter(train_input[:,0], train_input[:,1]) #전체 데이터
plt.scatter(25, 150, marker="^") #새로운 데이터
plt.scatter(train_input[indexes,0], train_input[indexes,1], marker='D') #새로운 데이터의 이웃데이터들
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
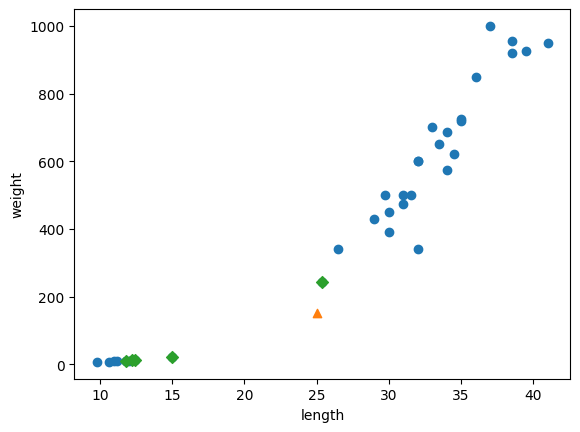
그래프상 근접한 데이터들은 도미데이터(1)이지만 예측수행시에는 빙어데이터(0)들이 많은 영향을 주는 것으로 보인다.
왜 일까? 이는 x축, y축의 범위 때문이었다.
( x축(길이)의 범위 : 10~40 / y축(무게)의 범위 : 0~1000 )
=> y축의 범위가 너무 커서 y축으로 조금만 멀어져도 매우 동떨어진 데이터로 인식하게 된다.
plt.xlim(범위) : x축의 범위를 지정하는 함수 => x축의 범위를 1000까지 늘려서 y축과 비례하여 비교해보자
plt.scatter(train_input[:,0], train_input[:,1])
plt.scatter(25, 150, marker="^")
plt.scatter(train_input[indexes,0], train_input[indexes,1], marker='D')
plt.xlim((0, 1000)) # x축의 범위(limit)를 0~1000 사이로 맞춤
plt.xlabel('length')
plt.ylabel('weight')
plt.show()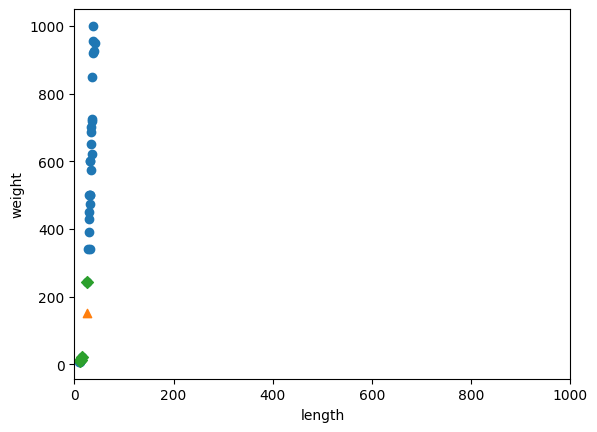
이는 x축의 scale이 y축의 scale에 비해 훨씬 작아서 y축만 고려의 대상이 된 것이었다.
=> 둘의 scale을 맞춰주는 작업필요
* 스케일링(Scaling) : 두변수의 크기(scale)을 맞춰주는 작업 -> 데이터 단위의 차이에서 오는 오류를 제거
[ 보편적인 스케일링 기법 ]
1) 정규화(normalization) : 값의 범위를 0~1사이의 실수로 옮긴다.
2) 표준화(standardization) : 표준편차, 평균을 이용해서 값의 범위를 정규분포 내로 옮긴다.
열(axis=0)을 기준으로 평균과 표준편차를 계산한다.
import numpy as np
mean = np.mean(X_train, axis=0)
std = np.std(X_train, axis=0)
train_scaled = (X_train - mean) / std
new = ([25,150] - mean) / std
plt.scatter(train_scaled[:,0], train_scaled[:,1])
plt.scatter(new[0], new[1], marker="^")
plt.xlabel('length')
plt.ylabel('weight')
plt.show()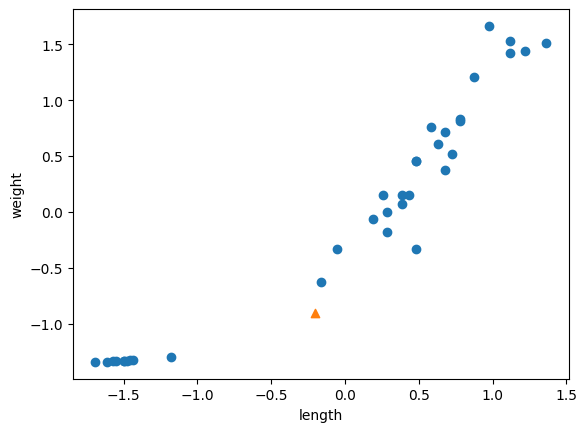
kn.fit(train_scaled, train_target)
test_scaled = (test_input-mean) / std
print(kn.score(test_scaled, test_target))
print(kn.predict([new])) #도미(1)로 분류스케일된 데이터로 학습(fit)과 테스트(test)해준다.
이후 예측하면 정상적으로 도미(1)로 분류가 되는 것을 볼 수 있다.
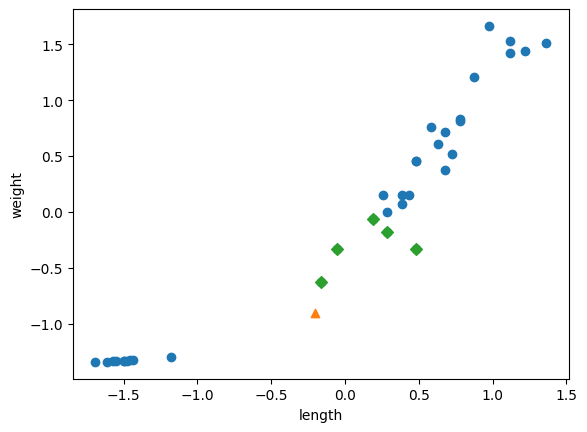
kn.neighbors([new])로 영향을 준 이웃을 분석해본 결과
그래프상으로 가까운 도미데이터(1)에 영향을 받아 도미로 분류했음을 알 수 있다.
StandardScaler : 표준화를 자동으로 진행해주는 사이킷런 라이브러리
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(train_input)
train_scaled = ss.transform(train_input)
test_scaled = ss.transform(test_input)
회귀(Regression)
:: 입력데이터로부터 연속된 숫자값을 예측
* 회귀의 matric(성능지표)
분류의 경우 accuracy 이용한다. (몇개의 class를 맞추었는가) 반면, 회귀의 경우 결정계수와 MAE라는 특정 지표를 이용한다.
1) 결정계수(R2) = 1 - ( 오차의 제곱합 / 편차의 제곱합 ) => 성능이 좋을 수록 1에 가까워진다.(%로 환산용이)
:: KNeighborsRegressor 라이브러리의 sore메서드의 반환값
from sklearn.neighbors import KNeighborsRegressor
knr = KNeighborsRegressor()
knr.fit(train_input, train_target)
print(knr.score(test_input, test_target)) # 결정계수2) MAE( Mean Absolute Error ) = Mean(|target - pred|) = Mean(|y - \hat y|) => 평균적으로 다른정도(g)
MSE( Mean Squared Error )와 유사한 개념
:: mean_absolute_error 라이브러리 함수를 이용
from sklearn.metrics import mean_absolute_error
test_prediction = knr.predict(test_input)
mae = mean_absolute_error(test_target, test_prediction)
print(mae)
0. 회귀모델을 이용해서 농어(perch)의 길이에 따른 무게를 예측해보자
# 농어의 길이와 무게 데이터
perch_length = np.array([8.4, 13.7, 15.0, 16.2, 17.4, 18.0, 18.7, 19.0, 19.6, 20.0, 21.0,
21.0, 21.0, 21.3, 22.0, 22.0, 22.0, 22.0, 22.0, 22.5, 22.5, 22.7,
23.0, 23.5, 24.0, 24.0, 24.6, 25.0, 25.6, 26.5, 27.3, 27.5, 27.5,
27.5, 28.0, 28.7, 30.0, 32.8, 34.5, 35.0, 36.5, 36.0, 37.0, 37.0,
39.0, 39.0, 39.0, 40.0, 40.0, 40.0, 40.0, 42.0, 43.0, 43.0, 43.5,
44.0])
perch_weight = np.array([5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0, 110.0,
115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0, 130.0,
150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0, 197.0,
218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0, 514.0,
556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0, 820.0,
850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0, 1000.0,
1000.0])
# 훈련세트와 테스트세트로 분할
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(perch_length, perch_weight, random_state=42)
#머신러닝이용을 위해 2차원 행렬로 reshape
train_input = train_input.reshape(-1,1)
test_input = test_input.reshape(-1,1)
print(train_input.shape, test_input.shape)
1. K-최근접회귀(K-Nearest Neighborhood Regression)
: 예측하려는 샘플에 가장 가까운 값 k개의 평균을 예측값으로 이용한다.
from sklearn.neighbors import KNeighborsRegressor
knr = KNeighborsRegressor()
knr.fit(train_input, train_target) #학습
print(knr.score(test_input, test_target)) #테스트
print("길이 50일 때 예측 무게 : ", knr.predict([[50]])) #예측1 : [1033.33333333]
print("길이 100일 때 예측 무게 : ", knr.predict([[100]])) #예측2 : [1033.33333333]그런데, 길이가 50cm일때, 길이가 100cm일때 모두 같은 무게를 예측한다.
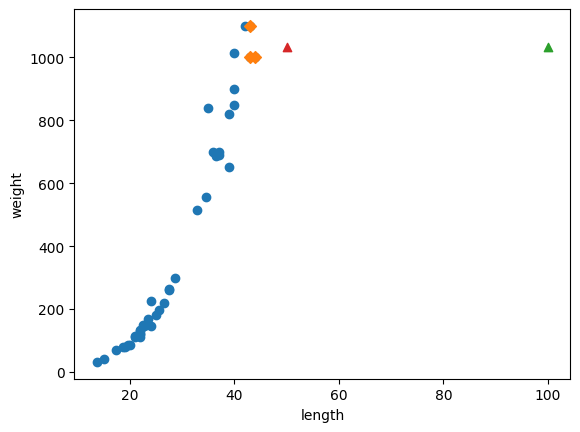
2. 선형회귀( linear regression )
: x와 y를 선형관계로 간주하고 그 선을 찾는 학습을 진행한다.
학습 데이터셋을 표현하는 y=ax+b의 직선을 찾는과정을 훈련한다.
모델 파라미터인 기울기 w, bias b를 가진다.
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(train_input, train_target) #학습
plt.scatter(train_input, train_target) #학습데이터 분포
plt.plot([15, 100], [15*lr.coef_ + lr.intercept_, 100*lr.coef_ + lr.intercept_], color="r") #red 선형선 그리기
plt.scatter(50, lr.predict([[50]]), marker="^") #길이 50의 예측
plt.scatter(100, lr.predict([[100]]), marker="^") #길이 100의 예측
plt.xlabel("lenght")
plt.ylabel("weight")
plt.show()plt.plot( [x값1, x값2] , [y값1, y값2], color옵션 )
lr.predict([[x값]]) : 선형함수를 이용하여 해당하는 결과값 y값을 예측한다.
lr.coef_ : 기울기 저장(w)
lr.intercept_ : 편향저장(b)
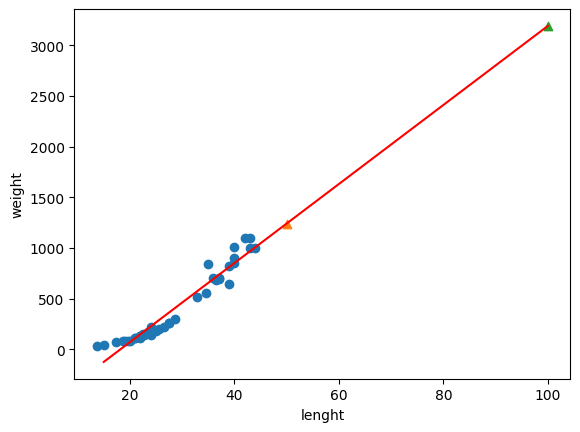
3. 다항회귀(Polynomial regression)
: 여러개의 weight을 가진 학습선을 찾아서 예측한다. n차함수의 곡선그래프를 이용한다.
train_poly = np.column_stack((train_input ** 2, train_input))
test_poly = np.column_stack((test_input ** 2, test_input))
print(train_poly.shape, test_poly.shape)column_stack : 주어진 numpy 배열을 수직으로 쌓아 2차원 배열을 새로 생성
~~~~~~~~~~~~~~~~~~~~~~~추후추가~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
분류(Classification)
:: 데이터의 클래스를 예측하는 작업
- 종류
- 이진분류(Binary Classification) : 1 or 0 (맞다 or 아니다)로 분류, 즉 클래스가 2개인 경우
- 다중분류(Multi-class Classification) : 클래스가 3개 이상인 경우
=> 둘다 핵심은 확률화!!
- 데이터 프레임 : pandas
>> 행(row)과 열(column)로 구성된 2차원 테이블 형태의 데이터 구조)을 다루는 라이브러리
- pd.read_csv(): 외부 csv 파일을 읽어서 프로그램에 올림
- Dataframe.head(): 데이터프레임의 처음 5개의 행을 출력
- pd.unique(): 고유값을 추출(중복제거)
- Dataframe.columns: 데이터프레임의 컬럼 이름을 담은 리스트 반환
- Dataframe.columns.difference([column name]): 해당 컬럼 이름을 제외한 후
1. K-최근접 이웃 분류(K-Nearest Neighborhood Classification)
kn = KNeighborsClassifier(n_neighbors=3)
kn.fit(train_scaled, train_target)
proba = kn.predict_proba(test_scaled[:5])
print(np.round(proba, decimals=4)) # 소숫점 네 번째 자리까지 표시
########
[[0. 0. 1. 0. 0. 0. 0. ]
[0. 0. 0. 0. 0. 1. 0. ]
[0. 0. 0. 1. 0. 0. 0. ]
[0. 0. 0.6667 0. 0.3333 0. 0. ]
[0. 0. 0.6667 0. 0.3333 0. 0. ]]
########
distances, indexes = kn.kneighbors(test_scaled[:5])
print(train_target[indexes]) #영향을 준 이웃들모음
########
[['Perch' 'Perch' 'Perch']
['Smelt' 'Smelt' 'Smelt']
['Pike' 'Pike' 'Pike']
['Roach' 'Perch' 'Perch']
['Perch' 'Perch' 'Roach']]
#########predict_proba(x) : 클래스 별 확률을 반환 , 하나의 train data가 각 target data에 가질 수 있는 확률을 리스트로 반환
=> 이때 ( 클래스 수 / 영향받는 이웃수(k) )의 확률 값만 가질 수 있다.
( 3일 경우 1/3(0.3333), 2/3(0.6667), 3/3(1) 가능 )
2. 로지스틱 회귀(Logistic Regression)
: 선형방정식의 output값(y값)에 시그모이드 함수를 적용하여 확률화한다.
- 이진분류 -> 시그모이드 함수(Sigmoid)(=Logistic Function) :: 0.0~1.0 사이의 실수로 변환하여 확률화 / 입력값이 양수라면 0.5이상, 음수라면 0.5이하의 확률반환
# 이진 분류를 위해 클래스 2개만 추출 (도미, 빙어)
bream_smelt_indexes = (train_target == "Bream") | (train_target == "Smelt")
train_bream_smelt = train_scaled[bream_smelt_indexes]
target_bream_smelt = train_target[bream_smelt_indexes]
#학습
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
lr.fit(train_bream_smelt, target_bream_smelt)
#예측
print(lr.predict(train_bream_smelt[:5]))
print(lr.predict_proba(train_bream_smelt[:5]))1) predict값 : ['Bream' 'Smelt' 'Bream' 'Bream' 'Bream']
2) predict_proba 값 :
[[0.99759855 0.00240145]
[0.02735183 0.97264817]
[0.99486072 0.00513928]
[0.98584202 0.01415798]
[0.99767269 0.00232731]]
# 모델 파라미터
print(lr.coef_, lr.intercept_)
#weight값 [-0.66280298 -1.01290277 -0.57620209 -0.4037798 -0.73168947]
#bias값 [-2.16155132]선형회귀식 y = -0.662 * (Weight)-1.01 * (Length)-0.576 * (Diagonal)-0.403 * (Height) -0.731 * (Width) -2.161 을 의미한다.
from scipy.special import expit
#decision값 : 선형회귀식을 통해 얻은 값 = 각 클래스에 대한 점수(판정기준) = output y값
decisions = lr.decision_function(train_bream_smelt[:5])
# [-6.02927744, 3.57123907, -5.26568906, -4.24321775, -6.0607117 ]
#explit : 시그모이드 함수
print(expit(decisions))
[0.00240145 0.97264817 0.00513928 0.01415798 0.00232731]predict_proba 값 = decision값을 sigmoid한 값이다.
- 다중분류 -> 소프트맥스함수(softmax) : 여러개의 출력값을 확률화하는 함수(0.0~1.0)
- 관련 하이퍼 파라미터
- max_iter : 반복 횟수 -> 손실함수를 최적화시키는 횟수
- C : Regularization를 제어하는 변수(penalty) -> 복잡성을 부여하여 과적합방지
lr = LogisticRegression(C=20, max_iter=1000) # default: C=1, max_iter=100
#학습
lr.fit(train_scaled, train_target)
#예측
print(lr.predict(test_scaled[:5]))
proba = lr.predict_proba(test_scaled[:5])
print()
print(lr.classes_)
print(np.round(proba, decimals=3))예측 : ['Perch' 'Smelt' 'Pike' 'Roach' 'Perch']
전체 : ['Bream' 'Parkki' 'Perch' 'Pike' 'Roach' 'Smelt' 'Whitefish']
softmax값 :
[[0. 0.014 0.841 0. 0.136 0.007 0.003]
[0. 0.003 0.044 0. 0.007 0.946 0. ]
[0. 0. 0.034 0.935 0.015 0.016 0. ]
[0.011 0.034 0.306 0.007 0.567 0. 0.076]
[0. 0. 0.904 0.002 0.089 0.002 0.001]]lr.classes_ : 로지스틱 회귀(Logistic Regression) 모델에서 학습된 클래스(클래스 레이블)의 목록을 나타내는 속성(Attribute)
인공신경망 (MLP : Multi Layer Perceptron)
:: 선형 레이어(Linear)와 활성화 함수를 조합하여 다층으로 구성된 신경망 / 모든층이 FCL(fully conected layer)로 구성된다.
1. FashionMNIST 이미지 데이터셋을 가져와서 시각화하기
torchvision : pytorch기반 컴퓨터 비전작업 패키지, 이미지 데이터셋 로드 및 전처리에 이용
- transforms 모듈
- transforms.compose : 변환 단계를 가지는 파이프라인 생성
- transforms.ToTensor : 이미지를 torch tensor로 변환
- transforms.normalize : 이미지 데이터의 평균, 표준편차를 이용하여 정규화 ( 이미지 채널을 대상으로 함함)
* transforms.normalize((0.5,),(0.5,)) ::: 단일채널이미지(흑백이미지)의 평균, 표준편차를 0.5로 설정 => 채널값을 -1~1 로 정규화한다는 의미
- datasets 모듈
FashionMNIST : PyTorch의 torchvision 라이브러리에서 제공되는 이미지 분류 데이터셋 중 하나
의류 및 패션 관련 제품을 나타내는 28x28 크기의 흑백 이미지로 구성되며, 각 이미지는 10개의 클래스중 하나로 구분
datasets.FashionMNIST(root="저장주소", train=True/False, transfrom=지정, download=True)

torch의 DataLoader함수
: 데이터셋을 미니배치 형태로 효율적으로 로드하고, 데이터를 섞거나 병렬로 로드하는 등 다양한 데이터 로딩 작업을 수행
(*배치사이즈 = 배치에 포함되는 데이터의 수 , 미니배치수 = 데이터를 묶은 배치의 수)
import torch
from torchvision import datasets, transforms
# Define a transform to normalize the data
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))])
# Download and load the training data
trainset = datasets.FashionMNIST('~/.pytorch/F_MNIST_data/', download=True, train=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True)
# Download and load the test data
testset = datasets.FashionMNIST('~/.pytorch/F_MNIST_data/', download=True, train=False, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=64, shuffle=True)plt.subplots() : 여러 개의 서브플롯(subplot)을 포함하는 그림(figure)을 생성하는 함수 ( *default : num_rows=1, num_cols=1 / 1행 1열 )
def imshow(image, ax=None, title=None, normalize=True):
"""Imshow for Tensor."""
if ax is None:
fig, ax = plt.subplots()
image = image.numpy().transpose((1, 2, 0))
if normalize:
mean = np.array([0.485, 0.456, 0.406])
std = np.array([0.229, 0.224, 0.225])
image = std * image + mean
image = np.clip(image, 0, 1) #clip : image의 각 배열요소가 0~1사이의 값만을 가지도록 제한
ax.imshow(image)
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.tick_params(axis='both', length=0)
ax.set_xticklabels('')
ax.set_yticklabels('')
return aximage, label = next(iter(trainloader)) #다음데이터배치를 가져와 -> 이미지, 라벨(클래스정답) 저장
imshow(image[0,:]) #이미지 배치에서 첫번째 이미지만 가져옴
2. Neural Network 모델을 생성
기본적으로 torch.nn의 모듈을 상속받아 모델을 만든다.
모듈이 제공하는 계산그래프, bp기능, dropout기능을 편리하게 이용할 수 있다.
import torch.nn as nn
class Classifier(nn.Module):
def __init__(self):
super().__init__() #상속받기
self.fc1 = nn.Linear(784, 256)
self.fc2 = nn.Linear(256, 128)
self.fc3 = nn.Linear(128, 64)
self.fc4 = nn.Linear(64, 10)
def forward(self, x):
x = x.view(x.shape[0], -1) #view = resize / shape[0] = 배치사이즈 유지, 나머지 자동설정 (2차원으로)
x = F.relu(self.fc1(x)) #layer1
x = F.relu(self.fc2(x)) #layer2
x = F.relu(self.fc3(x)) #layer3
x = F.log_softmax(self.fc4(x), dim=1) #output layer
return x #로그확률행렬반환
nn.Linear( in_features, out_features ) : 선형함수를 통해 가중합을 수행하는 모듈 ( in_f 차원벡터 -- 가중치(w) --> out_f 차원벡터 )
nn.forward(x) : 모델 객체를 호출할때 함수처럼 실행
- Module의 view() : 텐서의 모양을 변경하거나 평탄화(flatten) : 3차원 텐서를 2차원 행렬화, 배치 사이즈 유지
- torch.nn.functional.relu() : 양수는 그대로, 음수는 0을 출력하는 활성화 함( 양수에만 )
- torch.nn.functional.log_softmax()
- feature의 형상 : 784차원 벡터(1*28*28의 input_feature) -> 256차원 벡터 -> 128차원 벡터 -> 64차원 벡터 -> 10차원 벡터
- weight의 형상 : W1(784*256) -> W2(256*128) -> W3(128*64) -> W4(64*10) 의 weight들을 거쳐가도록 설계
3. 최적화 및 학습
-torch.optim : 최적화 알고리즘 모듈
-torch.nn.functional : 신경망 연산 모듈
import torch.optim as optim
import torch.nn.functional as F
model = Classifier() #모델생성
criterion = nn.NLLLoss() #로스함수(목적함수) 생성
optimizer = optim.Adam(model.parameters(), lr=0.003) #
epochs = 50
steps = 0
train_losses, test_losses = [], []
for e in range(epochs): #에폭단위
running_loss = 0
model.train() #모델을 학습모드로 전환 (기본적으로 평가모드) -> 드롭아웃, 배치정규화 등이 활성화
for images, labels in trainloader: #배치단위
optimizer.zero_grad() #모델가중치의 gradient를 0으로 초기화
log_ps = model(images) # 순전파(forward pass) - pred
loss = criterion(log_ps, labels) # 손실함수의 계산 - pred, target
loss.backward() #역전파 ( backward pass), 그래디언트 계산
optimizer.step() #가중치 업데이트
running_loss += loss.item() # 배치당 손실값 계산
# validation step - 현모델을 평가
test_loss = 0
accuracy = 0
model.eval() #모델을 평가모드로 전환 -> 드롭아웃, 배치정규화 등의 off
# Turn off gradients for validation, saves memory and computations
# 자동 미분을 꺼서 pytorch가 쓸 떼 없는 짓을 안하게 한다. (어차피 test set에서 하는 작업이므로)
with torch.no_grad(): #그래디언트(기울기) 계산을 비활성화하는 맥락함수
for images, labels in testloader: #배치단위
log_ps = model(images)
test_loss += criterion(log_ps, labels)
# 로그 확률에 지수 적용 ( 로그확률 -> 원래확률 )
ps = torch.exp(log_ps)
# topk는 k번째만큼의 큰 숫자를 찾아내는 것이다.
# dim=1 는 dimension을 의미한다. -> 두 번째 차원(열)을 기준으로 찾는다.
top_p, top_class = ps.topk(1, dim=1) # top_p : 최대값(최대확률), top_class : 인덱스
# labels를 top_class와 똑같은 형상으로 만든다음에 ---> 얼마나 같은게 있는지 확인한다.
equals = top_class == labels.view(*top_class.shape)
#equals 텐서 : 각 샘플에 대해 모델의 예측과 실제 정답이 일치하는지 여부를 담은 텐서
# equals를 float으로 바꾸고 평균 정확도를 구한다.
accuracy += torch.mean(equals.type(torch.FloatTensor))
train_losses.append(running_loss/len(trainloader))
test_losses.append(test_loss/len(testloader))
print("Epoch: {}/{}.. ".format(e+1, epochs),
"Training Loss: {:.3f}.. ".format(running_loss/len(trainloader)),
"Test Loss: {:.3f}.. ".format(test_loss/len(testloader)),
"Test Accuracy: {:.3f}".format(accuracy/len(testloader)))
4. 오버피팅 방지를 위한 drop-out처리
%matplotlib inline
%config InlineBackend.figure_format='retina'
import matplotlib.pyplot as plt
plt.plot(train_losses, label='training loss')
plt.plot(test_losses, label='Validation loss')
plt.legend(frameon=False)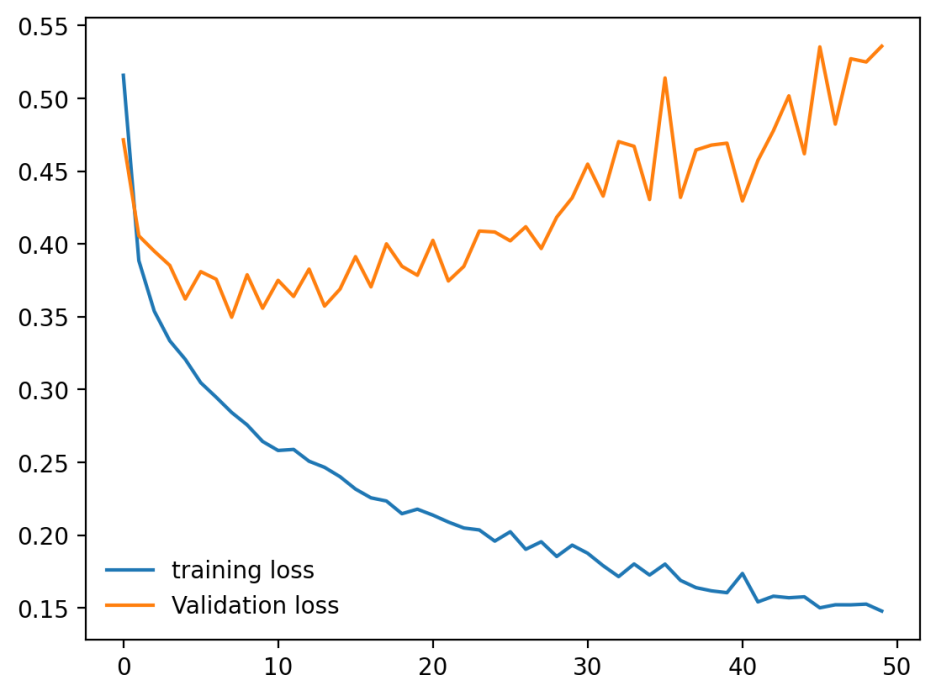
모델성능을 시각화해보니 epoch수가 커질수록 training loss는 줄어들지만 validation loss는 증가중이다.
=> overfitting의 발생!! 모델이 training data에 과적합된 상태이다.
class Classifier(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(784, 256)
self.fc2 = nn.Linear(256, 128)
self.fc3 = nn.Linear(128, 64)
self.fc4 = nn.Linear(64, 10)
# 0.2정도를 무작위로 골라 dropout한다.
self.dropout = nn.Dropout(p=0.2)
def forward(self, x):
x = x.view(x.shape[0], -1)
x = self.dropout(F.relu(self.fc1(x)))
x = self.dropout(F.relu(self.fc2(x)))
x = self.dropout(F.relu(self.fc3(x)))
# output은 dropout하면 안된다..
x = F.log_softmax(self.fc4(x), dim=1)
return x과적합을 방지하는 여러 방법중 drop-out 방식을 이용하여 모델코드를 수정한다.
nn.Dropout(p=dropout정도) : 훈련과정에서 무작위로 선택된 일부 뉴런을 비활성화 시킨다.
이때 마지막 out layer는 필수적으로 수행해야하는 로그확률출력이므로 drop-out처리에서 제외시킨다.
다시 test수행.. ( 이때 model.eval()에서는 drop-out이 자동적으로 멈춤(p=0) 즉 테스트는 모두 진행한다는 것 )
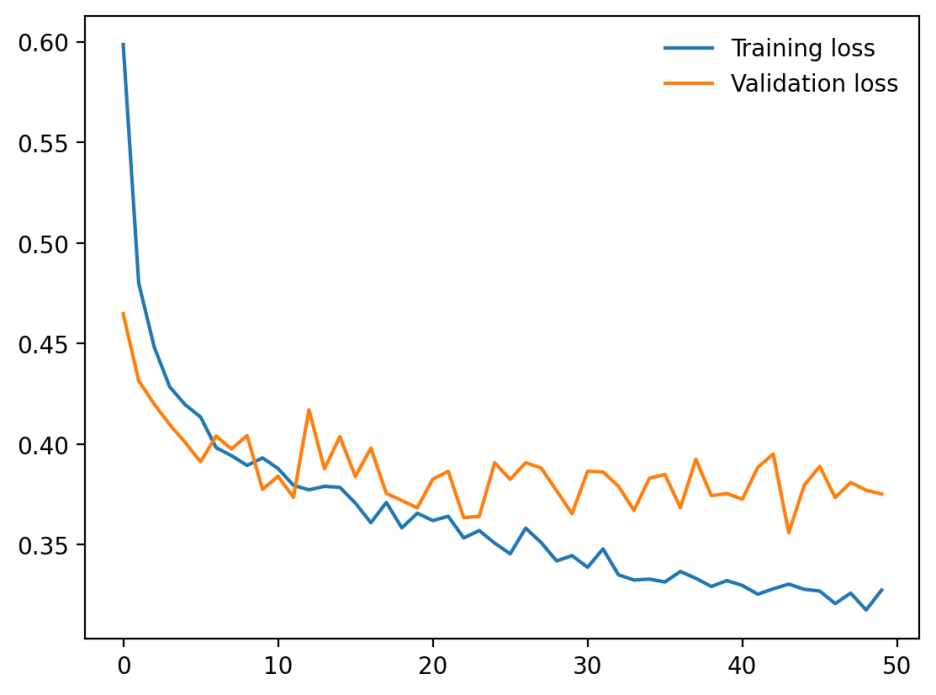
drop-out 이후 다시 학습한 결과물
에폭 증가에 따라 training loss와 함께 validation loss도 함께 감소하는 바람직한 형태를 보이고 있다.

'machine learning & deep learning' 카테고리의 다른 글
| [프로젝트 회고] PytorchLightning기반 딥러닝 프로젝트 - 데이터전처리 (0) | 2024.07.19 |
|---|---|
| RNN(순환신경망), LSTM(장단기메모리) 실습 : 주가분석, 영화리뷰분석 (0) | 2024.03.10 |
| Computer vision에서의 딥러닝 : OpenCV & U-net (0) | 2024.03.10 |
| 합성곱신경망 : CNN(conventional Neural Network) (0) | 2024.03.10 |